Elastic Collisions Inspiration...

date: 11 Apr, 2010, actionscript: 3 FP10, complexity: , feedback (votes):

Hi there,

Last weekend I had some spare time for writing an article I got in mind from long time ago, this is about Elastic Collisions, pretty much simple concept but apparently there are some people implementing it in the wrong way (I heard about some crazy exceptions, many bugs and problems people have) and in most of these cases it is because of they are detecting collisions in a wrong workflow. When we speak about elastic collisions we are speaking about the response of it after the collision happens and not when it actually happens (its detection), you must be careful in the way how you detect when the collisions occur, one think is detecting when the collision happens and other completely different is what happen after it.

First time I worked with elastic collisions was using actionscript 2, after many tests I did the performance of all these formulas were quite good due to its simplicity of how it works. The main concept is quite simple; an elastic collision is a collision between two objects (bodies which have mass) where the total momentum of the objects colliding are preserved. In other words, none of the energy involved in the collision is lost; it is distributed between the action objects depending on their mass and speed they got when the collision happened.

If you google about "elastic collisions" you may find thousands of articles and information around but unfortunately not all of this is correct, there are many people out there "as usual" explaining things in the most complicated way. I didn’t find any simple website where we can find out and understand about it easily or maybe I wasn’t lucky enough. I recommend to you take a look on the content published in Wikipedia if you want to know a bit more about it, it is really simple and well explained over there, they tell you how it works and also covers some aspects of 2 and 3 dimension collisions, the link is Elastic collision, note that the elastic collision formulas always deal with the response once the collision happens, you have to detect when the collision happen by yourself which is not hard but can be tricky to sort out when you’re facing many objects colliding at the same time.

Anyway the formula applied in one dimension (linear) is pretty much this:

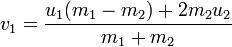and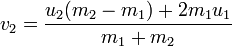

Wait!! Don’t run away! It is so simple to interpret it, basically what it says is; if we have two objects A and B and the object A has a mass of 3 Kilograms and it is moving with a speed of 1 meter/sec and the Object B which has a mass of 1 Kilogram is moving at 2 meters/sec, What will happen when these two objects collide? Which are the new forces (speed) for each? easy...

That’s all you need to know about it. Departing from this point I have made the following example using Flash Develop and the Open Source Flex SDK, the source of it is here download sourcecode. This example shows how the elastic collision can be implemented in flash in a very, very simple way; the whole program doesn’t have more than 30 instructions, I think that it really worth to have a go with it.

And then here is something interesting I found by chance at the science museum in London one day I was walking nearby and I decided to take a quick look inside. I met a machine that made me come back later with my camera and make a short video of it. This is a short video (no longer than 2 minutes) but I think enough for explaining what it is about and its connection with elastic collisions. After you watch it, you will be able to understand what the next experiment is about:

Well, when I saw that crazy machine (Energy ring by soda.co.uk) the first thing that came to my mind was if it was actually using elastic collision or not, and I was wondering if it is possible to simulate its behaviour in flash using simply elastic collisions. My approach on this experiment is totally oriented to the movement algorithm and the collision between the blocks you can see on the video, so things like the small particles flying around and the text on the display panel are not begin treated here, this is 100% oriented to the collision behaviour applying some gravity on the objects inside a circular path, I hope you see my point. Here is the sourcecode if you want to take a look on it. I think this source code is pretty much the same of the previous example apart of moving objects in a circle rather than on the x axis and colliding between these two limits (the walls), here they just collide between them and also I’m applying gravity taking advantage of the sine curve. Does it look similar to the video? I think that it is quite much what we can achieve using elastic collisions.

What about 2D elastic collisions?

Another approach of this elastic collision concept could be the collisions between balls, think about a billar pool game, the collision between the balls of a pool game is pretty much an authentic elastic collision with some extra factors that makes everything harder to achieve when coding a game such as; the friction of balls with air and on the table surface plus the spinning effect that they could have when moving that alters completely the collision response. I've been working long time ago on a game that unfortunately I never got the chance of finish. It is about an "8 ball" pool game using 15 balls and handling elastic collisions between them (without ball effects). So, here is what I have done so far, in this unfinished version I’m not making any validations about the game, it is just a free table all the time, hit what ever you want and then if put the white ball in a pocket I just put it back to the table behind the line. Unfortunately the source code is quite old, rusty and messy and is not available for downloading but I promise it will be as soon as I have a chance to tidy it up a bit. Take a look on it.

When we are speaking about physics, may be the most important thing about it, is to know when things exactly happen. It is quite important detect collisions in the right way, fast (in terms of performance) and highly responsible in terms of accuracy. The way how I'm detecting the balls collisions in the previous experiment is using the following function that by the way It doesn't use Math.sin and Math.cos functions at all which makes everything runs much faster.

Here is this function in practice... drag and drop components to find out how does it work.

And then if you’re wondering what the response of the collision using elastic collisions is, here is the function I used for it and also for predicting the white ball path before you hit it:

These functions are quite fast in term of performance, they don’t use Math.sin and Math.cos at all, I hope this article is useful to someone, it took me ages of research to find out all this information you can find here, if you use some of this code don't forget to make a donation (a beer), cheers!

Your name :

(not required)

Your email :

 @  (not required) not revealed

Your URL :

(not required)

Message (maximum 1000 chars) :

 

Confirm code :